Blackjack! For QLearning
This is the forth entry in my series of Unity for AI Education. Code is available for this and all other projects on my GitHub (username MLivanos), released under an MIT license.
Explore the inner workings of the Q-Learning algorithm for blackjack, a classic casino game where two players receive a hand of two cards and the goal is to get a value of 21 without going over. Aces count as either 1 or 11 - whichever helps you the most. Each player has the opportunity to ask for another card (Hit) or stick with the hand they have (Stand), and whoever is closer to 21 while remaining under 21 wins.
Q-Learning Algorithm
Here, we will train a Q-Learner for this task. Q-Learning is a machine learning algorithm that explores a problem/game by simulating it many times and tries to determine if actions will be positively or negatively rewarded for a particular state - for example, is it a good idea to hit or stand when you have 17 and your opponent is showing a 6? While the algorithm is conceptually simple, it has many hyperparameters that can be difficult to wrap your head around the first time you see the Q-update formula:
Q(s,a) = (1-α)Q(s,a) + α(reward + γ*max(Q(s))
Here, α is the learning rate, a number between 0 and 1 which basically asks how quickly we want to learn something. A low α may result in a slow learning Q-learner, while a high α may result in an algorithm that constantly changes its mind about what is good or bad at for a particular state-action pair.
On the other hand, γ is the discount factor, a number between 0 and 1 that asks how much we want to value future rewards compared to immediate rewards. While future rewards may sound just as important as immediate rewards, consider the blackjack example we are learning from. Is it good to hit on 17? Well, we might get closer to 21! But that isn't guaranteed, so we need to consider the possible future reward of getting closer to 21 with some skepticism.
To top it off, we also have another parameter ε which says how often we want to trust the Q-learner and how often we want to explore randomly. Why would we want to explore randomly? Well, imagine it's your first day at a new school and you don't know how to get to class. You wander around and eventually find a route that gets you there, and you start taking that route regularly. One day, you get bored and take a different turn and find a shortcut! Because you chose to explore new possibilities instead of exploiting your existing knowledge, you stumbled upon a new route that saves you time. In the same way, we want our learner to occasionally try something new and possibly learn something.
But when should we try something new and when should we use the knowledge we have? In Q-Learning, this is decided by the following:
Choose a random number r between 0 and 1.
if r < ε : exploit - do what the Q-Learner says is best otherwise : explore - take a random action
So how do we set epsilon? Well, we would imagine we would want to do a lot of exploration in the beginning - we don't have a lot of knowledge so it doesn't make sense to exploit it. Eventually, as we learn more and more, we should trust ourselves more and more to make good decisions. To simulate this, we introduce two new hyperparameters, min-ε and ε-decay, and set epsilon by:
ε = max(ε*ε-decay^(number of games we played), min-ε)
Basically saying we will always explore at least min-ε percent of the time, and gradually exploit more and more as we learn.
So, we have five hyperparameters to chose:
- α : the learning rate
- γ : the discount factor
- Initial ε: the initial exploration factor
- ε-decay: how quickly we chose to trust our knowledge
- min-ε: the minimum amount of exploration we will do during training
How do we even begin to understand how to do that?
Our Tool: Q-Learning Visualizer
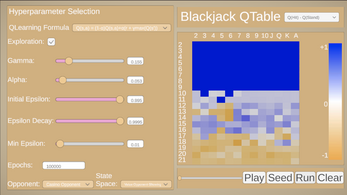
Here, we have a tool for exploring the different parameters of the problem. First, choose your state-space. What information do you want to give the Q-Learner? How's about the value of their current hand? Simple enough, but can we give it more information? Maybe the card the opponent is showing? But is the card important, or just the value of the card? What are the consequences of choosing on vs another? Does one perform better than another, or does one make more "mistakes" than the other? Then, add hyperparameters one by one to see how each of them (or the lack of each of them) can result in a better or worse final table, in smoother or rougher training.
After selecting which state space, Q-Learning formula you want to use (choose from a simple "learn to predict immediate rewards" function to the more complex function defined above), and the values for hyperparameters, click "Run" to simulate the game for the number of episodes you chose.
The Q-Table is presented with your value as rows and the opponent's showing card as columns, with color denoting how your agent you learned to play that particular state. By default, you see the Q-Table on a spectrum from orange to blue, where bluer means the learner thinks it's better to hit, orange means it's better to stand, and white is more neutral. You can change this view by clicking the dropdown menu and selecting what you want to see, such as the Q-Values for a specific action (hit or stand), or the policy, a binary hit or stand depending on which Q-value is greater. Use the slider to see how the strategy evolved over time.
Ask yourself: what happens when I train the simple Q-Learner? Why does it fail? Why does adding a learning rate allow for smoother training? What do you notice about how the discount factor impacts low-value states? What does adding exploration do to the final result? What is the implication of using different state spaces?
There is one last button of interest, which is the "Seed" button. Maybe it isn't immediately clear when you should hit or stand, but it is clear for certain values. If you have a value of 21, you should stand. If you have a value. of <=11, it is impossible to lose on a hit. "Seed" initializes the Q-Table to reflect this, possibly allowing for easier training.
Finally, when you train a Q-Learner you like, click the "Play" button to play against it yourself! How does it do?
Good luck with your machine-learning educational goals!
| Status | Released |
| Platforms | HTML5 |
| Author | ProdigiousMike |
| Genre | Educational, Simulation |
| Made with | Unity |
| Tags | artificial-intelligence, casino, machine-learning, reinforcement-learning, Unity |



Leave a comment
Log in with itch.io to leave a comment.